We can start to model the knowledge of a domain describing (the models of) the concepts existing in that domain. This is the role of concept descriptions in Noos. The concepts described can be concrete (like a patient) or abstract (like a syndrome, or a prototypic patient). We will introduce concept descriptions syntax from simple to more complex--the syntax used in this chapter is summarized in BNF at the end of the chapter in § 2.7 and the complete syntax in in Appendix A.
A description is a list composed of the define token, a name (identifier), and some slots. A slot is a list with a feature name and a value. The value can be simply a name of a description defined elsewhere. The overall concept we are defining is called the root of the description. A description of root A with feature names X and Y and values V and W looks like this: (define A (X V) ...(Y W)). Since Noos evaluation is lazy (also called non-strict or on-demand) you may (while constructing a description with define) refer by name to a description not yet defined without causing an error. The following Example 2.1 is an example of three concept descriptions.
Names of concept descriptions are symbols, and there is no difference on the case of the letters used. For instance, Nick, nick, NICK and nICK are all valid and equivalent. Descriptions can be defined 1) in a file and then the file is to be loaded into the Noos environment or 2) by directly typing them on the Noos listener. If we type Nick's description on the listener the returned value is <Nick>, which is the ``print-name'' of the description--and not the identifier symbol. See Chapter 8 for more details on the Noos environment.
The feature name is a name for a relation between
concepts. In the example above, father, mother and children
are such relations linking concepts John, Nick, and Mary.
In a sense, descriptions are a way to group together--to
modularize--relations. The common syntax to write relations is with a
predicate name, as in father(x, y) or father(John, Nick). A
description groups together all the relations that have as first parameter
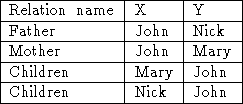
a specific concept. In the case of John the description assembles
father(John, Nick) and mother(John, Mary). The usual way to describe
relations is as tables, as shown below. The predicate representation syntax
mirrors this tabular representation, since for every row of a relation R there
is a corresponding term R(X, Y).
In fact, mother and father are an special kind of relations--binary
relations with unique image (many-to-one mapping). These relations are called
functions and the usual mathematical syntax
for them is 
. John's description can be more accurately
described as assembling those function names whose domain is John,
i. e. 
and 
. In the knowledge
representation literature, this kind of relations grouped together in
``frames'' have been called features.
Summarizing, a description
clusters together (as slots) the features
in which is involved as domain (if we think in terms of functions)
or as first parameter (if we think in terms of relations).
However, there is a small complication clearly in view: children is a
relation but is not a function--children has not a unique image
since there may be more than one concept being the children of somebody.
This issue can be solved by representing binary relations as functions over
sets--i. e. representing R(x, y) by 
.
Because of this, Noos allows slots where the feature value is a set.
The syntax for feature set values is the enumeration of references--as
in the example that follows where
.
So far for binary relations, but what about representing n-ary relations?
Bluntly put, descriptions are n-ary relations. In relational
representation persons can be defined as relations, for instance
person(father,mother,spouse,children) can be a model of ``person''. The
names of variables are immaterial since only the arity and the position for
each argument is important--thus 
is exactly
the same relation (it is a syntactic variant). In descriptions,
however, names are important since a description can be seen as a n-ary
relation where arguments are given by name instead of by
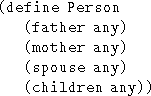
position
. The person relation above would be a
description as the following one (where any stands for any value, as
will be explained later).
However, it is not clear how we could represent John in such a
relational representation as . If we try we try
to represent John as 
we have problems--it is
not a complete instantiation. This is because an important property of
feature terms and descriptions: they can convey partial
information. In the case of John the description conveys information
about fathers and mothers, but not about spouses, children, or other facts
of persons like profession or birthdate. Certainly, using relational
representation we can represent partial information: we have to crack the
n-ary relation into smaller (maybe binary) relations. For instance using
predicates like person(x), father(x,y), spouse(x,z), etc. However,
this is not the point here, since we were merely interested in justifying
intuitively the capability of having n-ary relations--and the advantage of
representing partial information.
