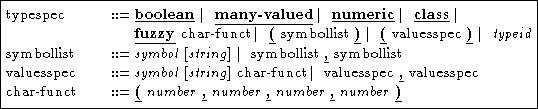
Figure 4: Syntax of type definition.
The type is the only attribute that is mandatory in a fact declaration. It determines the set of values a fact can take. For instance the fact dead would be a boolean predicate (it is false or true); and the facts temperature and voltage should be of numeric type.

Figure 4: Syntax of type definition.
A fact is valuated over the set of values determined by its type plus the special value unknown, meaning ignorance of the value. There are four basic predefined types, namely boolean, many-valued, numeric and class; and a parametric user-defined type named fuzzy. Moreover, programmers can declare two anonymous types by enumerating the values that the fact can receive, namely set and linguistic. Next there is a summary of the meaning of Milord II fact types:
fever = Type: many-valued
The type many-valued is parametric with respect to a set of linguistic terms, representing truth values, defined by the programmer. This set of terms must be defined in the inference system declaration (see Section 4). The value of facts of this type will be an interval over the so defined ordered set of linguistic terms.
The values of facts with an associated fuzzy set are still intervals of linguistic terms. The way of computing the interval will be done, in this case, by the application of the fuzzy membership function to the numerical value of the fact that must appear in a relation named needs_quantitative.
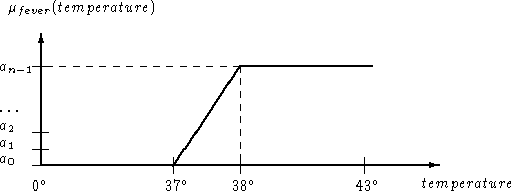
Figure 5: Fuzzy set representing the concept fever.
We can see an example of fact declaration of the concept fever (see Figure 5). This concept is declared by giving the four points of the trapezoidal approximation of its membership function.
fever = Type: fuzzy (37,38,43,43)
Relation: needs_quantitative temperature
Attributes of relations will be explained in Section 3.1.4.
Facts of this type get values from a user-defined finite set of symbolic values. This set is defined by enumerating its elements. For instance, the fact treatment gets values from a set of antibiotics ( etambutol, aciclovir and ganciclovir). This set is, moreover, the anonymous type of the fact treatment.
treatment = Type: (etambutol, aciclovir, ganciclovir)
The value of the fact treatment will be a mapping from the
elements of its type to intervals of linguistic terms representing the
degree of membership of every antibiotic to the fact
treatment (v.g. ![]() ).
).
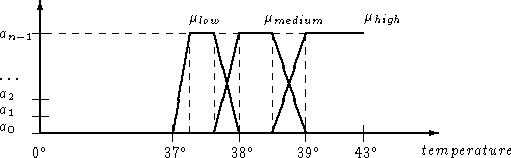
Figure 6: Fuzzy sets representing the concept fever.
The declaration of this new interpretation of the fever concept can be:
fever = Type: (l "low" (37,37.3,37.6,38),
m "medium" (37.6,38,38.5,39),
h "high" (38.5,39,43,43))
Relation: needs_quantitative temperature
Notice that, as in the case of fuzzy facts, it is necessary to declare the same relation needs_quantitative with a numeric fact, in this case again temperature. The optional string in the elements of the type (e.g. low) is used only for informational purposes.