In this section we present a parametric family of many-valued calculi for rule specialisation. Each calculus is determined by a particular algebra of truth-values belonging to a parametric family of algebras that is described next.
Throughout this paper, an Algebra of truth-values 
will be a finite linearly
ordered residuated lattice with a negation operation, that is:
, 
) is a chain of n elements:
where 0 and 1 are the booleans False and
True respectively.
is a unary operation defined as 
, the
only definable order-preserving involutive mapping in 
, i.e. it holds: 
.
:
then 
for all c
is defined by residuation with respect
to T, i.e.
Such an implication
operator satisfies the following properties :
if, and only if, 
then 
and
As it is easy to notice from the above definition, any of such
truth-values algebras is completely determined as soon as the set of
truth-values and the conjunction operator T are
chosen. So, varying these two characteristics we generate a family of different
multiple-valued logics. For instance, taking 
or
we get the well-known Gödel's and
ukasiewicz's semantics (truth-tables) for finitely-valued
logics [6, 7, 8, 9].
In the following we describe the language, the semantics and the
deduction system (specialisation calculus) of a particular logic
corresponding to a given algebra 
.
The propositional language 
is defined by:
,
consisting on a set of propositional variables
plus true,
, and
= Mv-Literals( 
) 
Mv-Rules( ), where:
):
):
):
and q are literals, V is an interval of truth
values in , and
}
That is, sentences of 
, which will be generically called
mv-formulas, are indeed signed formulas under the form of pairs
of usual propositional formulas (restricted to be literals or rules)
and intervals of truth-values.
Notation conventions. We shall commonly use:
Further, a, b, ...
will denote truth-values from while V, W, ... will denote
intervals of
truth-values. For simplicity we shall also write 
to
denote
the mv-formula 
.
The semantics is obviously determined by the connective
operators of the truth-value algebra . Interpretations
are defined by valuations 
mapping the (propositional) sentences
to truth-values of fulfilling the following
conditions
:
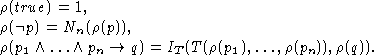
Having truth-values explicit in
the sentences enables us to define a classical satisfaction relation in spite
of the models being multiple-valued assignments.
The satisfaction relation between interpretations and mv-formulas
is defined as
iff 
and it is extended to a semantical entailment between sets of
mv-formulas and mv-formulas as usual:
iff for all
such that 
, for all 
.
Taking into account the motivations introduced in the previous section, the deduction system we consider for rule specialization in our many-valued logical framework is the following one.
Remark:
In the above description of the Specialization inference rule we are
assuming 
. It is understood that if
n = 1 then the specialization rule of inference turns out into the following
modus ponens inference rule: from (p, V) and 
infer
.
The notion of proof inside Mv-SC is defined as usual.
It is easy to check that the above specialisation calculus is sound.
Axioms A1 and A2 are trivially satisfied by any interpretation. Weakening, not-introduction, not-elimination and composition inference rules also trivially preserve truth. Let us check the truth preservation of Specialization rule for the simplest Modus Ponens case, i.e. when n = 1. We shall prove that
By definition, 
is the minimal
interval containing all the solutions of the following
family of functional equations:
for any 
, and 
. Suppose then that 
and let
a model of (p, U) and of
. Let 
and
. Then and . By
hypothesis, any solution for 
satisfying the equation
must be in W, so is also a model of (q, W).
On the other hand, it is obvious that the logic Mv-SC is not
complete. For instance, if we consider the two-valued case, i.e.
, we have 
but 
. It is also the case that the language is
not complete for literal deduction in general. For instance, we have 
but 
. However,
it can be shown that the system is complete for mv-atom deduction provided
we further restrict the language basically by not allowing negated literals in
the language. This restricted mv-atom completeness can be seen as a
many-valued counterpart of the completeness of classical modus ponens for
atom deduction with propositional Horn clauses. This will be shown in the next
subsection.
