In classical (boolean) rule bases, deduction is mainly based on the modus ponens inference rule:
In the case that A denotes a conjunction of conditions 
, the above inference rule is only applicable when every condition
of the premise, i.e. 
and 
, is satisfied, otherwise nothing can
be inferred. However, if we only know that condition is
satisfied, due to the well known logical equivalence 
, we can use partial
deduction to extract the maximum information from incomplete
knowledge in the sense of the following specialisation inference
rule:
The rule 
is called the specialisation of 
with respect to the proposition . Notice
that in the particular case that the rule has only one condition in
the premise, we may resort to the usual modus ponens rule.
The following are the corresponding functional specification of what a rule specialisation process is.
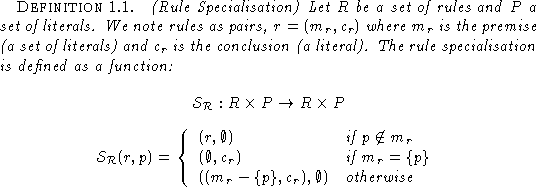
The extension to specialisation of agent's rule bases is straightforward.
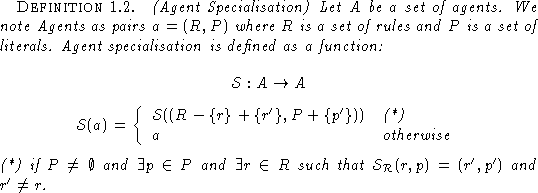
In other words, the specialisation of an agent's rule base consists on the exhaustive specialisation of its rules. Rules that only have one condition appearing in the set of literals will be eliminated and a new literal will be added. This new literal will be used again to specialise the agent. The process will finish when the agent has no rule containing on its conditions a known literal. This approach is different for instance from the logic programming one used in [13]. There, partial deduction is goal driven, whereas here partial deduction is data driven.
In this paper we propose the use of this technique to improve the communication behaviour between agents by allowing agents to answer a query with a part of the result of the specialisation of its rule base. In an approximate reasoning context we propose to extend the above boolean specialisation inference rule to encompass partial truth, for instance in the following way:
meaning that if is known to be true at least to the degree
and the rule is true at least to the
degree 
, then the specialised rule is true at
least to a degree 
, being f a suitable
combination function.
More concretely, in section 2 we formally describe both the semantics and syntax of a many-valued logical calculus for partial deduction of rule bases. Section 3 is devoted to the functional description of an agent specialisation mechanism. In section 4 an example on multi-agent medical diagnosis is presented, showing the usefulness of the communication mechanism based on specialisation. Finally, a discussion on the results is presented in Section 5.