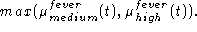Conditions

First of all we explain the conditions of the rules. In order to give an understandable explanation to the way conditions of rules are written, we do not consider conditions containing paths. The conditions of a rule can be written in affirmative form (condition) or in negative form ( no(condition)).

The elemental conditions can be:

1. A truth-value belonging to the set of linguistic truth values of the local logic of the module, including true or false. This is the most simple possible condition. Truth values evaluate to degenerated intervals, that is evaluates to . A possible use of this conditions is to give initial values to facts or to limit the conjunctive value of the premise of a rule. For instance, the next rule unconditionally gives the value [definite, definite] to the fact ciprofloxacine.

   R001 If true then conclude ciprofloxacine is definite

2. The name of a fact of type boolean, many-valued or fuzzy. For instance,

   R002 If pregnant then conclude vancomicine is possible

   where pregnant is a boolean concept.

3. Predicates over expressions containing facts of type numeric, set or linguistic.
   1. Numeric predicates

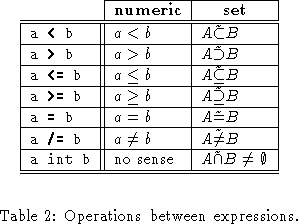
      A numeric expression is composed by numbers, numeric facts and arithmetic operations (+,-,*,:) shown in Table 1 with the meaning expressed in the first column. The evaluation of an expression of this type returns a number over which we can predicate with the predicates shown in Table 2, where the meaning is expressed in the first column.

      

      The valid predicates are < (less), > (greater), <= (less or equal), >= (greater or equal), = (equal), and /= (different). We decided to overload these predicates to reduce the number of total predefined predicates of the language. An example of use of these numerical predicates is:

      

      R003 If temperature > 39  then conclude fever is definite

   2. Set predicates

      We can build set expressions in a similar way as numerical expressions taking into account that the operations ``+'' and ``*'' are interpreted as the fuzzy set union and the fuzzy set intersection respectively. ``-'' and ``:'' are not applicable over set facts (see the second column of Table 1).

      The valid fuzzy predicates are < (subset), > (superset), <= (subset or equal), >= (superset or equal), = (equal), /= (different) and int (intersection degree). The binary predicates apply over the evaluations of two expressions of the same type. The evaluation of these predicates is, as before, an interval of truth-values. We give the sense of the predicates for fuzzy sets in the second column of Table 2. To get the mathematical details of the predicates refer to [21]. For instance, considering the following rule,

      R004 If treatment int (etambutol,ganciclovir) then conclude ...

      the operation int (fuzzy intersection degree) is applied between two fuzzy sets, the first one corresponding to the value of the fact treatment (that is, a membership value for each element of ( etambutol, aciclovir, ganciclovir)), and the second one a fuzzy set with the elements etambutol and ganciclovir with value true and the others (in this case only aciclovir) with value false.

   3. Linguistic predicates: Linguistic variables, together with linguistic values, are used to build predicates of the form ``linguistic_variable is linguistic_value''. For instance:

      R004 If fever is high then conclude ...

      Given a numerical value s for the variable fever, the predicate fever is high returns the value of .

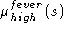      It is also possible to define more complex linguistic predicates of the form ``linguistic_variable is ( value_1 or value_2 or ...)". For instance:

      R004 If fever is (medium or high) then conclude ...

      Now, given a value s, the predicate fever is (medium or high) returns the value of: